Visions of the future: formal verification in Rust

May 22, 2024

In response to a recent Boats article, I mentioned that Rust’s type system drastically changes things for verification. This comment seems to have aroused a lot of interest, so I figured I’d expand on it, explaining how Rust simplifies formal verification and why this had the verification community excited for a while now.

I assume that most of you reading this post won’t be experts in formal methods so before we talk about what Rust brings to the table, I think it merits to explain what formal verification is and what problems it has. I’m a novice when it comes to blogging, but I’ll try to avoid too many technical details and keep things snappy – bear with me please.

what is formal verification?

The essence of formal verification is determining whether an object of study satisfies some specification. Often, these objects are programs of a certain language, and our specifications describe properties of the inputs and outputs of our programs. Let’s look at a trivial verification problem:

{ x = 0 }
x := 2
{ is_even(x) }

We surround our code x := 2 by two state assertions in curly braces, the first is called the precondition and describes the state of our program before execution while the second is called the postcondition and describes what must be true after execution. We call these precondition-program-postcondition combinations Hoare triples. They are a standard syntax for stating and reasoning about the correctness of programs. The task of verification is then to prove that all states satisfying our precondition must also satisfy our postcondition – which in this case is evidently true.

Of course, verification problems are not as trivial as our first example, the languages we consider are more complex, and the programs we verify are larger, both of these make it difficult to scale verifiers In most cases, verifiers are working on undecidable problems due to Rice’s Theorem. Moreover, this is one domain where exponential worst-case runtimes are often considered fast. For example, SAT solvers run in exponential time and SMT solvers in general diverge. To make matters worse, often the reasoning that has to be performed is exponential in size to the program, without even getting solvers involved!. There’s one ‘feature’ in particular which causes problems for verification: pointers. Let’s look at a second slightly bigger example:

{ *x = 0 && *y = 0 }
*x = 1
{ is_even(y) }

Here our precondition tells us that both x and y are 0 before executing our program, so surely y must be even afterwards, right? But what if x = y? As anyone who’s written C or Java could tell you, mutable aliases abound, and are often the source of hard to debug issues like double-frees or iterator invalidations. This is – of course – a huge part of the motivation for Rust’s borrow checker, but we’re interested in a slightly different problem which in formal verification we call framing.

framing the problem

The frame of an operation refers to the parts of the state that are left unchanged, by that operation. If you can determine the precise frame of each operation, you can know which facts about your program are unaffected by it. Finding the appropriate frame is essential in verification; if we frame out (remove) too much information we won’t be able to finish our proof, but if we leave too much in, we’ll accumulate too much information and get stuck. The objective is to identify exactly what part of the state we need to enable local reasoning, shrinking the part of the state we need to consider at any point in time.

So long as your language is very simple (like BASIC) and has no mutable data structures, you can decide the frame syntactically by looking at the names of variables. Of course, any non-trivial imperative language will introduce some sort of pointer-like structure which makes determining the frame of an operation a semantic operation.

Tony Hoare already implicitly observed the problems pointers cause for framing in the 1970s, though he isn’t thinking of verification:

Worst still, an indirect assignment through a pointer, just as in machine code, can update any store location whatsoever, and the damage is no longer confined to the variable explicitly named as the target of assignment...

The additional of pointers means we need to reason globally about state, each modification to a pointer could invalidate arbitrary facts about our program. The framing problem effectively stalled work on the verification of imperative programs for decades.

separating resources

The turn of the millennium marked the beginning of a new era with the introduction of separation by O’Hearn and Reynolds Reynolds, John C. “Separation logic: A logic for shared mutable data structures.” Proceedings 17th Annual IEEE Symposium on Logic in Computer Science. IEEE, 2002. logic which builds upon the notions of logical resources first introduced by Girard for linear logic. In separation logic, we treat ownership of memory as a non-duplicable resource The power of separation logic in reasoning about memory has led to it being extended to reasoning about other kinds of resources, some of which might be (partially) duplicable, fractional or have other fun properties. Examples include reasoning about time steps, energy (like electricity), or security. , if I have ownership of some address a, I can’t also give you ownership of a, that would be like if I could turn one dollar into two. To combine resources we have a separating conjunction a &*& b which represents the combination of disjoint resources a and b (like two separate addresses).

The magic then comes from a new rule, pointedly called the Frame Rule, which says: If I can prove { P } C { Q } then I can prove { P &*& R } C { Q &*& R }, for any P, Q, and R. Another way to put it is that to say, if we can put aside R for a moment, then afterwards, we’ll still have R. This allows us to have local reasoning, each part of the program can now think only about the resources it actually needs without worrying about what its doing the the rest of the program state.

Looking at our example from earlier, if we state in separation logic we see how its easy to solve:

{ *x = 0 &*& *y = 0 }
*x = 1
{ is_even(y) }

All we have to do is frame out *y = 0, recovering it after we evaluate *x = 1.

Its hard to understate how much impact this “simple” change in perspective had. The following years saw an explosion of activity with this idea extended in every conceivable direction. 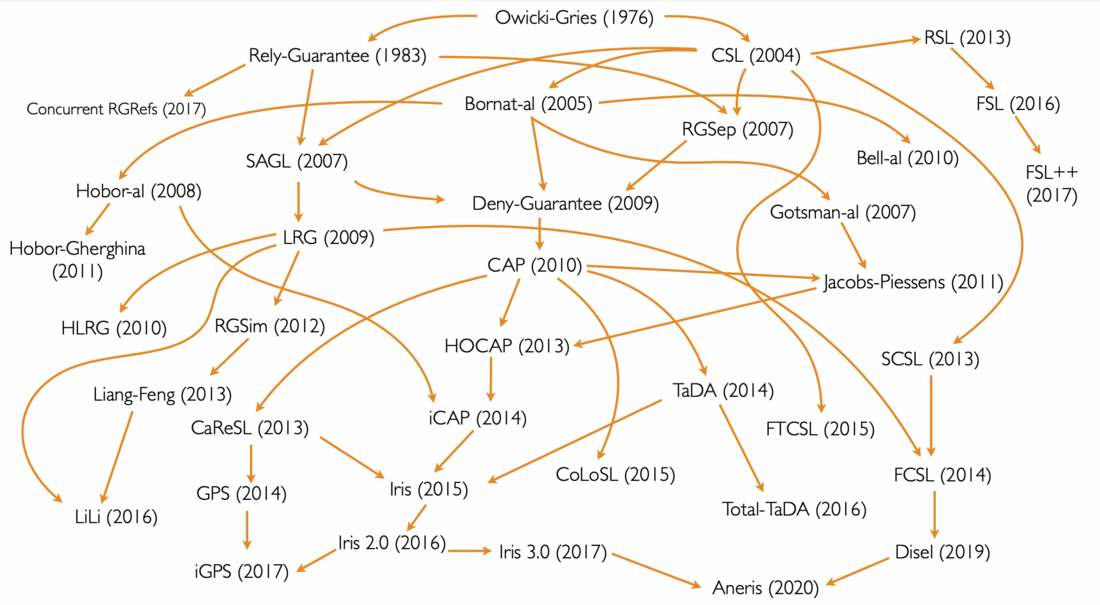The family tree of Concurrent Separation Logics (CSL). Note how after the introduction of CSL in 2004, works explode with almost every year having a major logic introduced, things only stabilize somewhat with the introduction of Iris. Many thanks to Ilya Sergey for the incredible graphic above

Modern separation logics like Iris are wonderfully powerful tools, allowing us to precisely state and reason about the most complex and subtle programs and properties. Using separation logic it becomes possible to build scalable verification tools for imperative languages like C, Java, Javascript, or even machine code.

why rust, then?

If separation logic is so great, why do formal verification researchers care so much about Rust?

Separation logic intertwines a memory safety proof into every verification proof; for example, to write to a pointer you must demonstrate ownership of that pointer. This both poses an aesthetic and practical problem, every step of proof must track which resources are used where, and which are being framed, hiding the essence of the proof’s argument and causing new issues for automation.

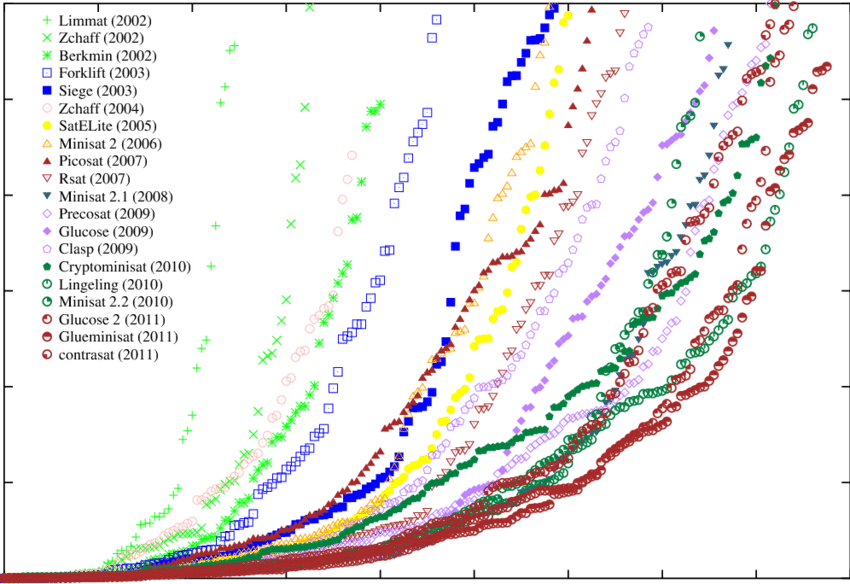
Separation logic wasn’t the only revolution which happened at the turn of the millennium, the same period saw the introduction of CDCL SAT solvers and modern SMT solvers, exponentially increasing our ability to solve propositional and first-order logical problems The x-axis is the number of solved problems while the y-axis is CPU time. Improvements from 2002 to 2011. Graphic from The HACMS program: Using formal methods to eliminate exploitable bugs.. In comparison, the automation for separation logic is in its relative infancy, and significantly harder to boot; separation logics tend to be in much tougher complexity classes than ordinary logics Compared to “ordinary” logics, separation logic is very hard, even simple fragments will be at best PSPACE-complete (much worse than EXP). Intuitively this is caused by how automation must track how it ‘spends’ its resources..

That’s where Rust enters the picture, the ideal target language for formal verification is one which allows us to keep the strengths of separation logic reasoning – its precise framing – while ditching its weaknesses – the tedious and sometimes difficult resource tracking. This would allow us to have good reasoning principles for complex imperative patterns while benefiting from the high-powered automation available for first-order logics.

As Ralf Jung once noted “Rust programmers already know separation logic”. Setting aside interior mutability for the moment, the ownership typing of Rust tells us that if we have two variables x : T and y : T they are always separated, the separating conjunction is baked into the language! Even better, Box<T> asserts exclusive ownership of a memory region for T, giving us our “points to” predicates.

In some sense, the Rust type checker is performing a separation logic proof for us, each time we compile our program. If we could rely on the Rust type system to guarantee memory safety and separation for us, freeing us from the need to do that in separation logic and instead allow us to focus on the core functional properties we want to prove The first tool to note this was Prusti (2019), which verifies Rust programs in a separation logic verifier but uses typing information to automate the separation logic parts of the proof!. Except that Rust has a core feature which seems to violate the strict separation that we so desire: borrows.

Like other forms of reference, borrows introduce an alias and thus cause problems for framing, when we do x = &mut y, there are now seemingly two ways to access the value of y, either through y or through *x. Here the Rust type system saves us again, the borrow checker tells that y cannot be used so long as x is around maintaining the principle that at most one name exists for each mutable value.

From the perspective of formal verification what this means is that we can reason exclusively in terms of x if after x’s lifetime expires we can “update” y to reflect the modifications made with x. This is very good, because we continue reasoning locally, we don’t have to model the effects that modifying x has on our heap, we can effectively pretend its an ordinary variable. This is exactly what’s done by formal verification tools like Creusot or Aeneas!

Both these tools use the Rust type system to eliminate the need for separation logic, in fact, these tools transform Rust programs into equivalent, pure, functional programs! Through this encoding they are able to leverage all the pre-existing tools for reasoning in first-order logics (SMT solvers for Creusot and Lean for Aeneas).

What’s even more fascinating about Rust is how some tools like Verus have gone even further and added separation logic back in after eliminating it. Verus has a notion of “proof mode” code, where you write code which Rust will borrow check, using the type system to handle the separation logic reasoning about code that potentially has nothing to do about memory safety! Rust has shown that maybe the borrow checker was what we needed to bring separation logic, and thus scalable verification to the masses!

conclusion

I hope I was able to convey some of why formal verification researchers are excited about Rust. There’s a lot more exciting stuff going on which builds upon and extends this foundation, and there’s also the question of what to do about unsafe Rust where this ownership discipline isn’t necessarily enforced. Those will have to wait for a separate post.

appendix: what about ocaml?

Why aren’t we able to eliminate separation logic from a functional language like OCaml then? Well, OCaml includes the ref type, which creates a mutable, aliasable reference, for the following example succeeds:

let x = ref 0 in
let y = x in
x := 5;
assert (!y = 5)

This means all the framing problems we had earlier appear again in OCaml. Combined with the module system of OCaml which lets you hide the implementation details of your types behind abstractions, mutable aliasing can be lurking anywhere in your program!

While in practice OCaml programs are often disciplined in their use of mutation, formal verifiers have to assume the worst: to prove { P } totally_not_evil (x : ref int) (y : ref int) { Q }, we need to consider every possible value for x and y, even those where they mutably alias. Unlike Rust, OCaml doesn’t (yet) have any notion of “unique reference” which could be used to recover nice reasoning principles.

Many thanks to Boris, Bouke, and Sacha for their comments, and Boats for the motivation to write.